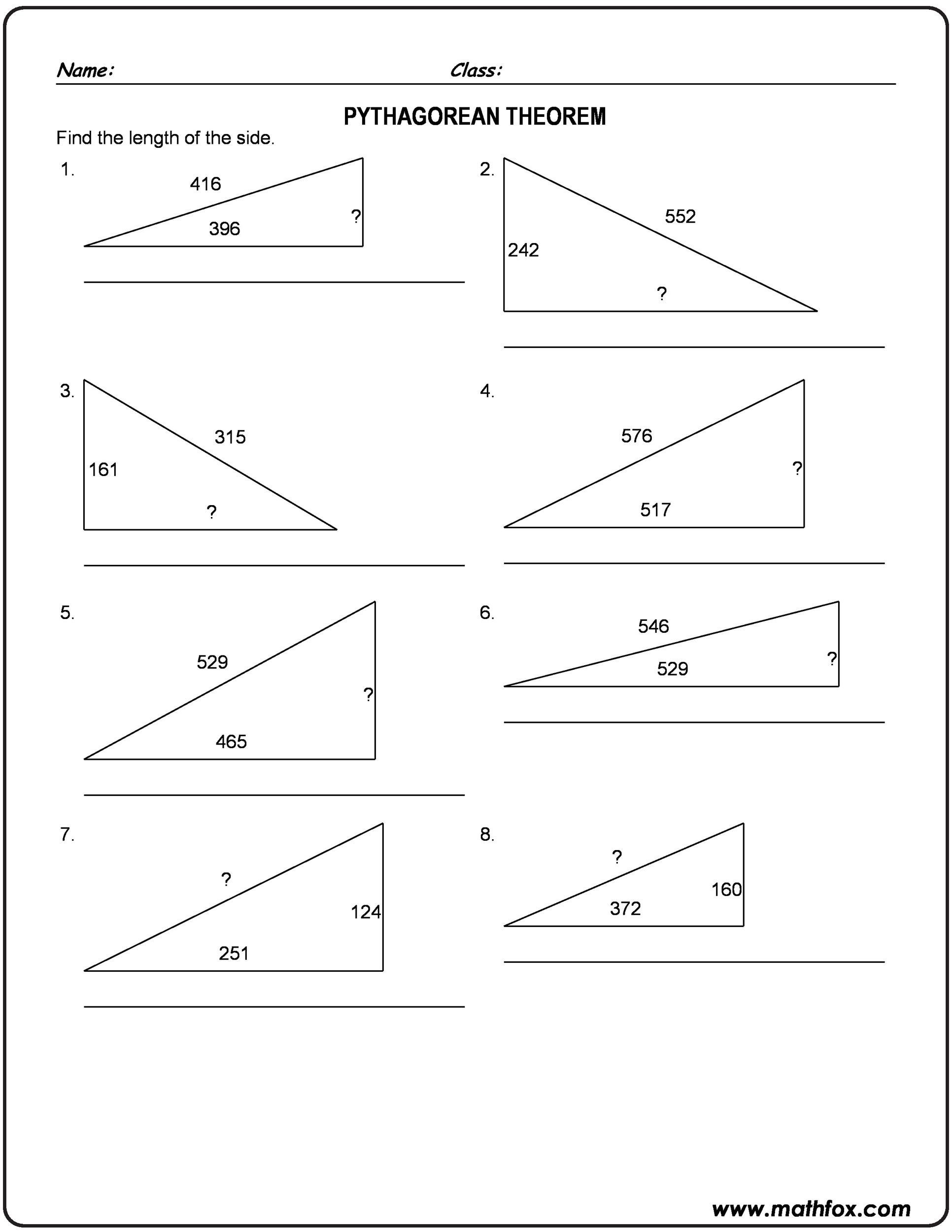
The simplicity of the Pythagorean Theorem worksheet is the best thing about it. What is the Pythagorean Theorem? Formulated in the 6th Century BC by Greek Philosopher and mathematician Pythagoras of Samos, Pythagorean Theorem is a mathematic equation used for a variety of purposes. Over the years, many engineers and architects have used Pythagorean Theorem worksheet to complete their projects.
Table of Contents
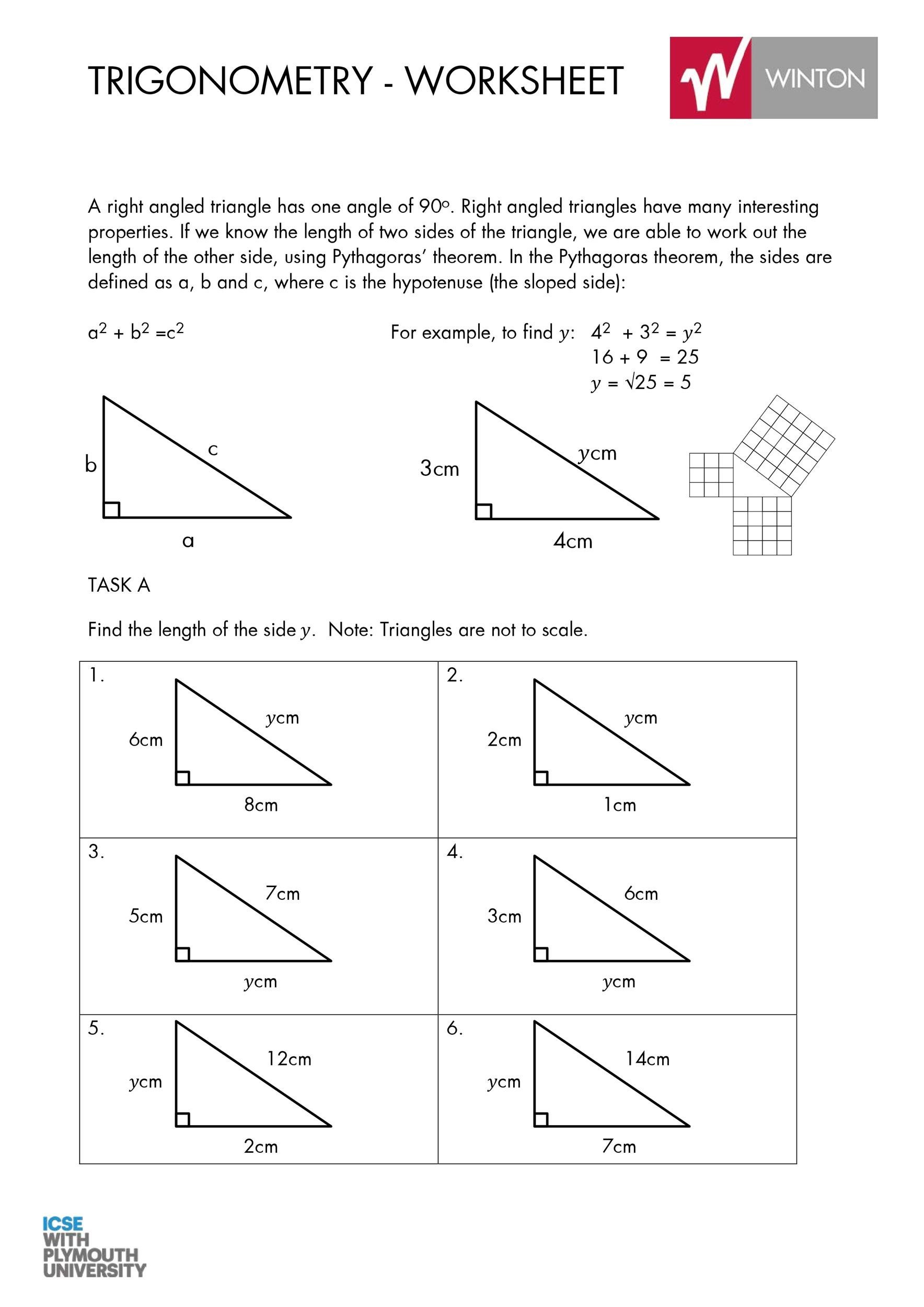
A simple equation, Pythagorean Theorem states that the square of the hypotenuse (the side opposite to the right angle triangle) is equal to the sum of the other two sides. Following is how the Pythagorean equation is written:
a²+b²=c²
In the aforementioned equation, c is the length of the hypotenuse while the length of the other two sides of the triangle are represented by b and a. Though the knowledge of the Pythagorean Theorem predates the Greek Philosopher, Pythagoras is generally credited for bringing the equation to the fore. This is the reason the Pythagorean equation is named after him. Before we discuss the Pythagorean Theorem and the Pythagorean Theorem worksheet in detail, let’s take a look at who Pythagoras of Samos was and how he came up with the Pythagorean equation.
Pythagorean Theorem Worksheet
Knowing Pythagoras of Samos and how he came up with the Pythagorean equation
A 6th century BC Greek philosopher and mathematician, Pythagoras of Samos is widely credited for bringing the Pythagorean equation to the fore. Though others used the relationship long before his time, Pythagoras is the first one who made the relationship between the lengths of the sides on a right-angled triangle public. This is why he’s regarded as the inventor of the Pythagorean equation.
Apart from being a philosopher and mathematician, Pythagoras founded the Pythagoreanism movement. Born in Croton, Italy, Pythagoras travelled to many different countries including Greece, Egypt, and India. After moving back to Croton in 530 BC, Pythagoras established some kind of school. He returned to Samos in 520 BC. It was in late 6th Century BC that Pythagoras started to make important contributions to philosophy and math. The Pythagorean equation was one of those contributions.
Though he revealed the Pythagorean equation to the world in the late 6th Century BC while living in Samos, many historians believe that Pythagoras first thought about the equation during his time in Egypt. In fact, according to many historians, Pythagoras learned geometry, the Phoenicians arithmetic and other branches of mathematics from the Egyptians.
Though he has made many important contributions to philosophy, Pythagoras is widely known as the founder of the Pythagorean Theorem. As previously mentioned, the Pythagorean Theorem is a mathematical equation that states that the square of the hypotenuse (the side opposite to the right angle triangle) is equal to the sum of the other two sides.
Today the aforementioned equation bears Pythagoras’s name but it’s important to know that he wasn’t the first one to use the equation. Before Pythagoras’s time, the Indians and the Babylonians utilized the Pythagorean Theorem or equation. Since they constructed the first proof of the theorem, Pythagoras and his disciples are regarded as the inventors of the equation.
Many historians say that Pythagoras worked in a very secretive manner. This is the reason little evidence is available that the Greek Philosopher/ mathematician himself worked on and proved the Pythagorean Theorem. It is important to note that the first time Pythagoras was given credit for the Theorem was five centuries after his death. This makes Pythagoras’s contribution to the Theorem even more debatable. Nonetheless, since Pythagoras is the only one connected to the Pythagorean Theorem known today, we have to give him due credit. Now that we’ve discussed who Pythagoras of Samos was and how he came up with the Pythagorean equation, it’s time to take a detailed look at the Pythagorean Theorem and the Pythagorean Theorem worksheet.
Understanding Pythagorean Theorem
According to Pythagorean Theorem, the sum of the squares on the right-angled triangle’s two smaller sides is equal to the side opposite to the right angle triangle (the square on hypotenuse). Using a Pythagorean Theorem worksheet is a good way to prove the aforementioned equation. An amazing discovery about triangles made over two thousand years ago, Pythagorean Theorem says that when a triangle has a 90° angle and squares are made on each of the triangle’s three sides, the size of the biggest square is equal to the size of the other two squares put together! A short equation, Pythagorean Theorem can be written in the following manner:
a²+b²=c²
In Pythagorean Theorem, c is the triangle’s longest side while b and a make up the other two sides. The longest side of the triangle in the Pythagorean Theorem is referred to as the ‘hypotenuse’. Many people ask why Pythagorean Theorem is important. The answer to this is simple: you’ll be able to find the length of a right-angled triangle’s third side if you know the length of the other two sides. This equation works like magic and can be used to find any missing value. Following is an example that uses the Pythagorean Theorem to solve a triangle.
a²+b²=c²
6²+8²=c²
36+64=c²
100=c²
c²=100
c=√100
c=10
In this equation, the longest side of the triangle ‘c’ is missing. By finding out the sum of the squares of the two other sides, we were able to find the missing value. The most famous mathematical contribution of Pythagoras, the Pythagoras Theorem was one of the earliest documented theorems. Though Pythagoras is given most of the credit for the theorem, a major contribution to the theorem was made by his students.
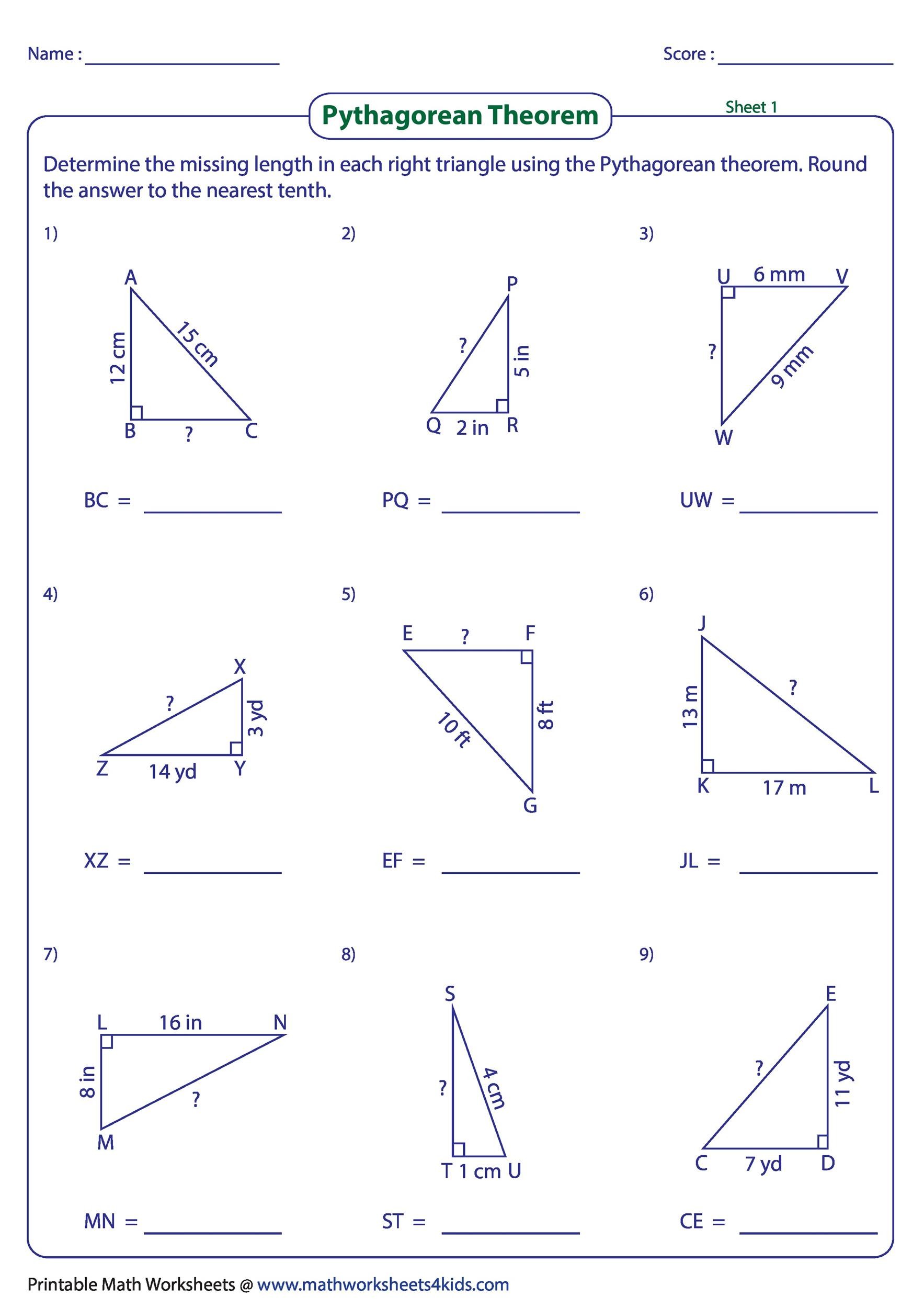
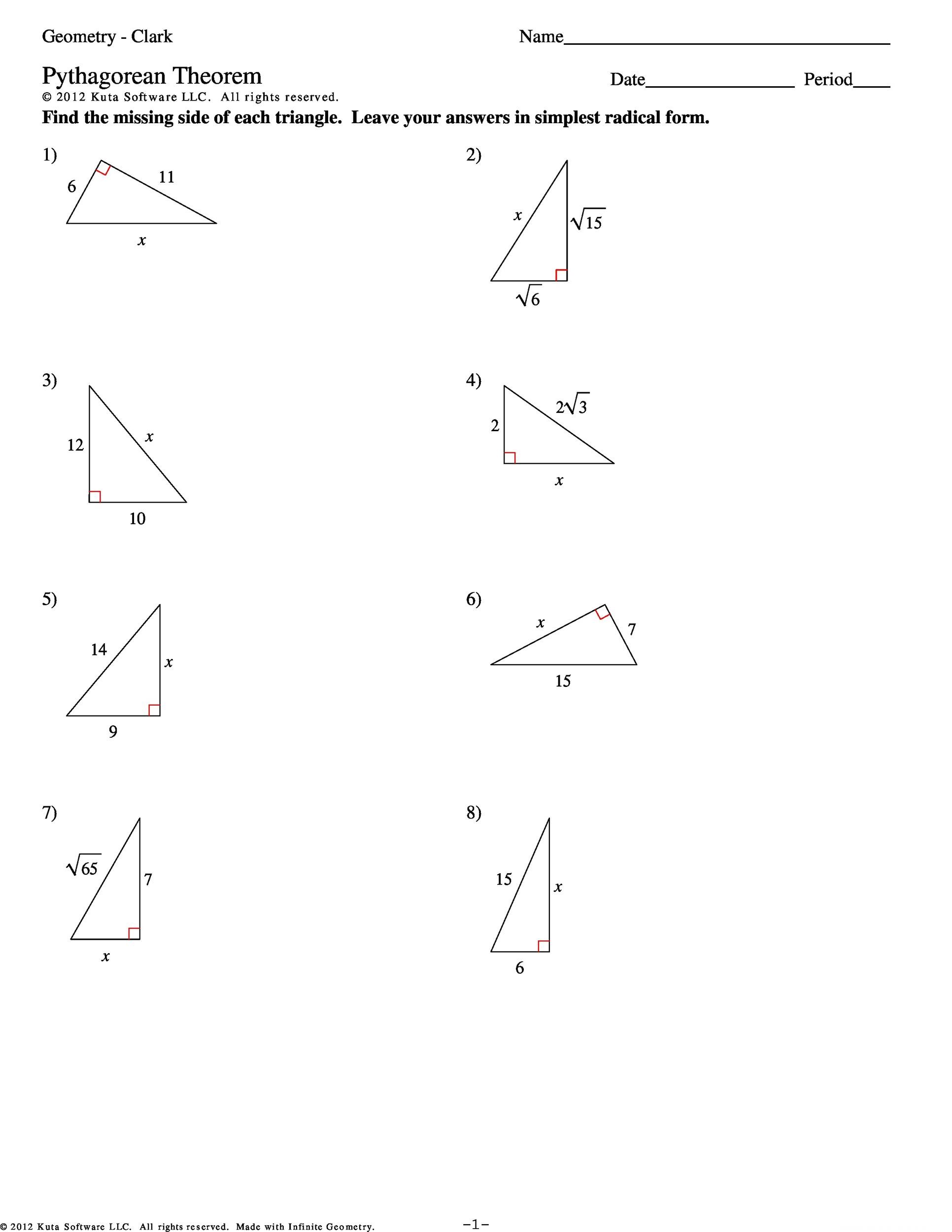
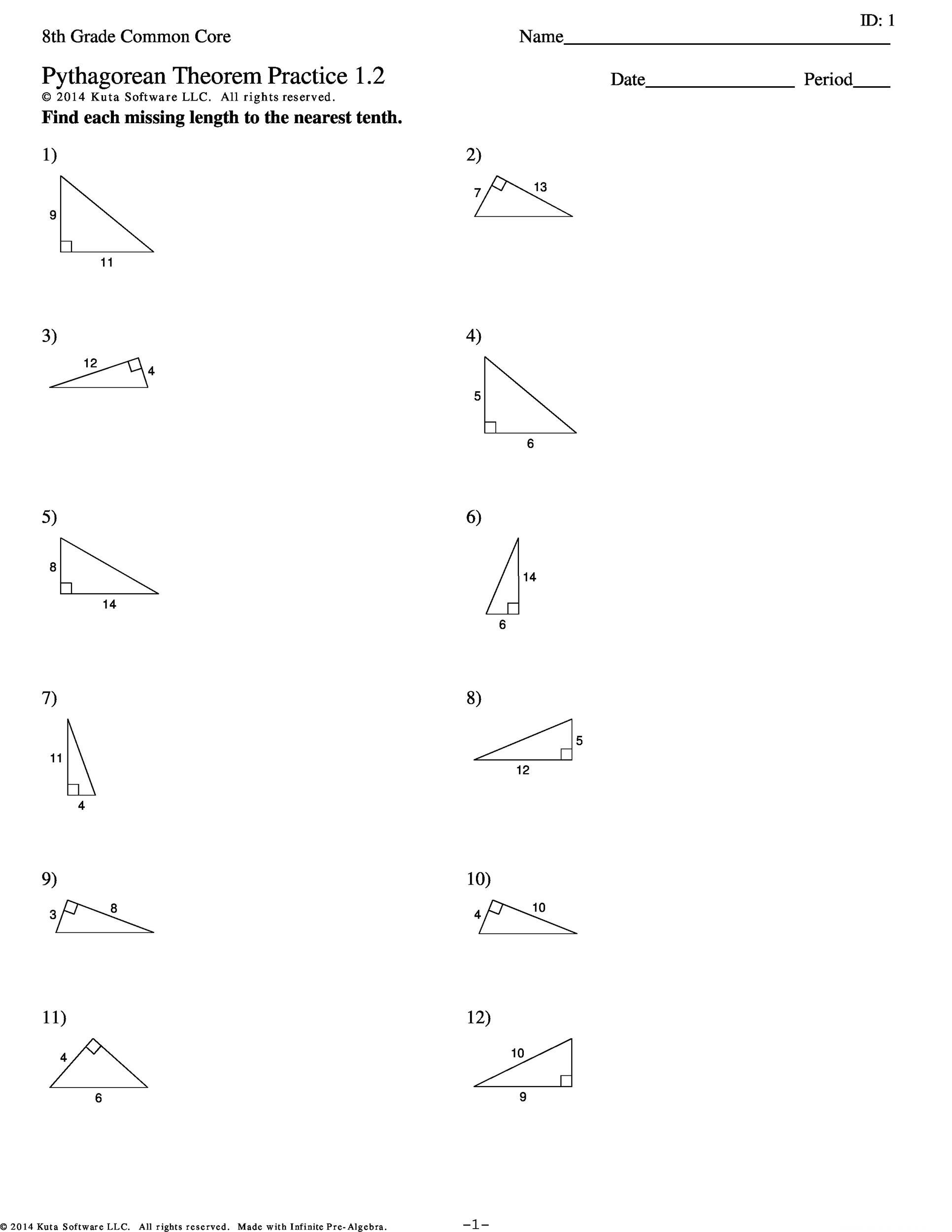
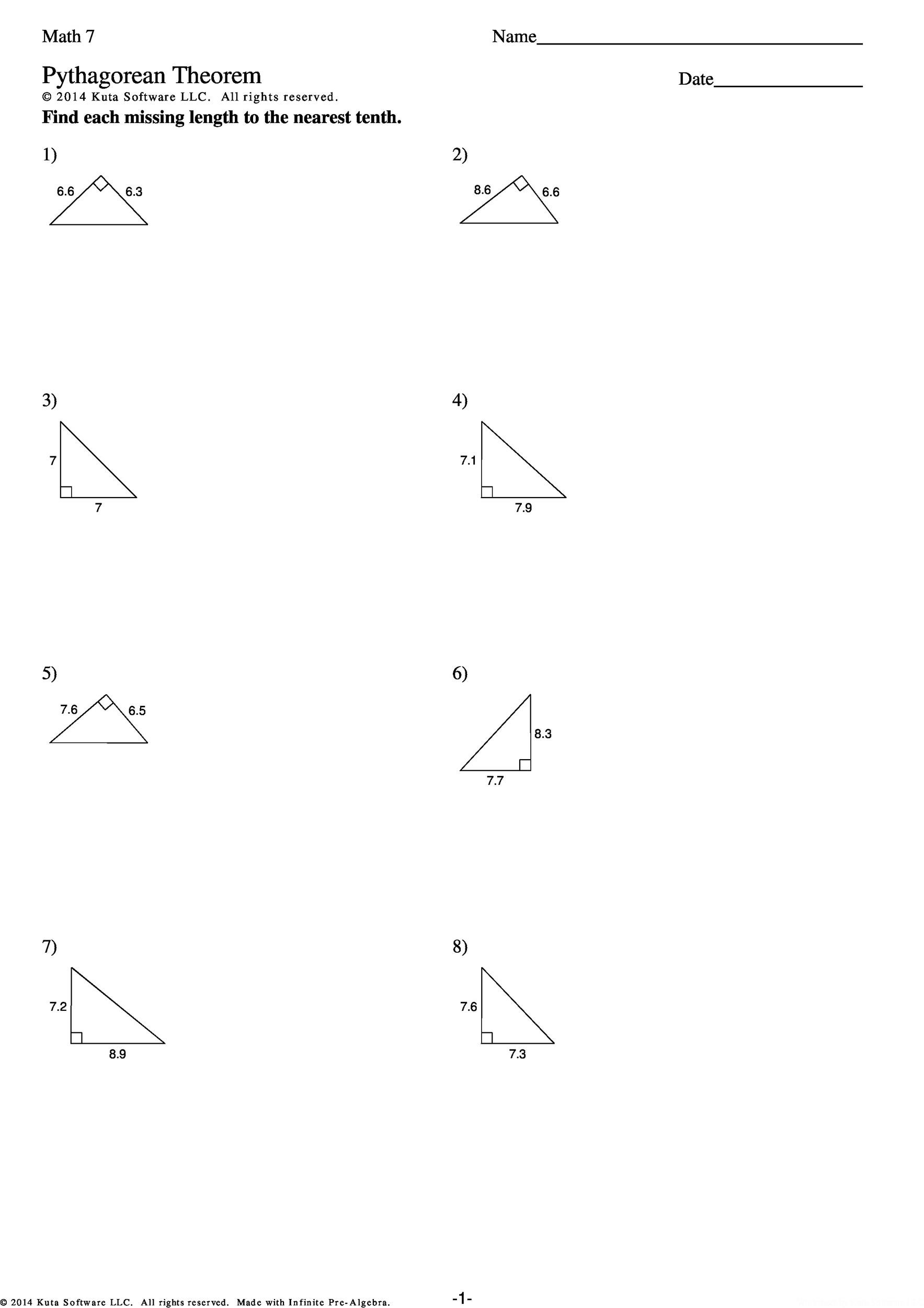
When you look at a Pythagoras Theorem worksheet, you’ll notice that the theorem enables you to find the length of any right angle triangle side provided you know the length of the other two sides. Also, using the theorem, you can check whether a triangle is a right triangle. The Pythagoras Theorem is extremely useful in solving many math problems. Further, you can use it in many real life situations. This is illustrated by a Pythagoras Theorem worksheet.
Pythagorean Theorem Word Problems Worksheet
Using Pythagorean Theorem worksheet
A good way to review the Pythagoras Theorem and expand the mathematical equation is using a Pythagoras Theorem worksheet. By using the worksheet, you’ll be able to get a good understanding of geometry. Additionally, the worksheet will give you an opportunity to review the knowledge related to the different types of triangles. Finally and most importantly, you’ll be able to practice the ancient equation invented by the Greek mathematician and philosopher, Pythagoras. Before you start using the Pythagoras Theorem worksheet, just remember that ‘c’ is the hypotenuse while the shorter sides of the triangle are represented by ‘a’ and ‘b’.
A Pythagoras Theorem worksheet presents students with triangles of various orientations and asks them to identify the longest side of the triangle i.e. the hypotenuse. As you know by now, the formula used in Pythagoras Theorem is a²+b²=c². Regardless of what the worksheet asks the students to identify, the formula or equation of the theorem always remain the same. Though, the students could be presented with different challenges including solving triangles:
- Labeled in different order
- With a different set of letters
- By using vertices to name the sides
The symbols used in the Pythagoras Theorem are something students will find on their calculators. Figuring out how to use these functions is what students need to establish. There is involvement of the Babylonians and the Egyptians in the invention of the Pythagoras Theorem but the earliest known proof of the theorem was produced by the school of Pythagoras.
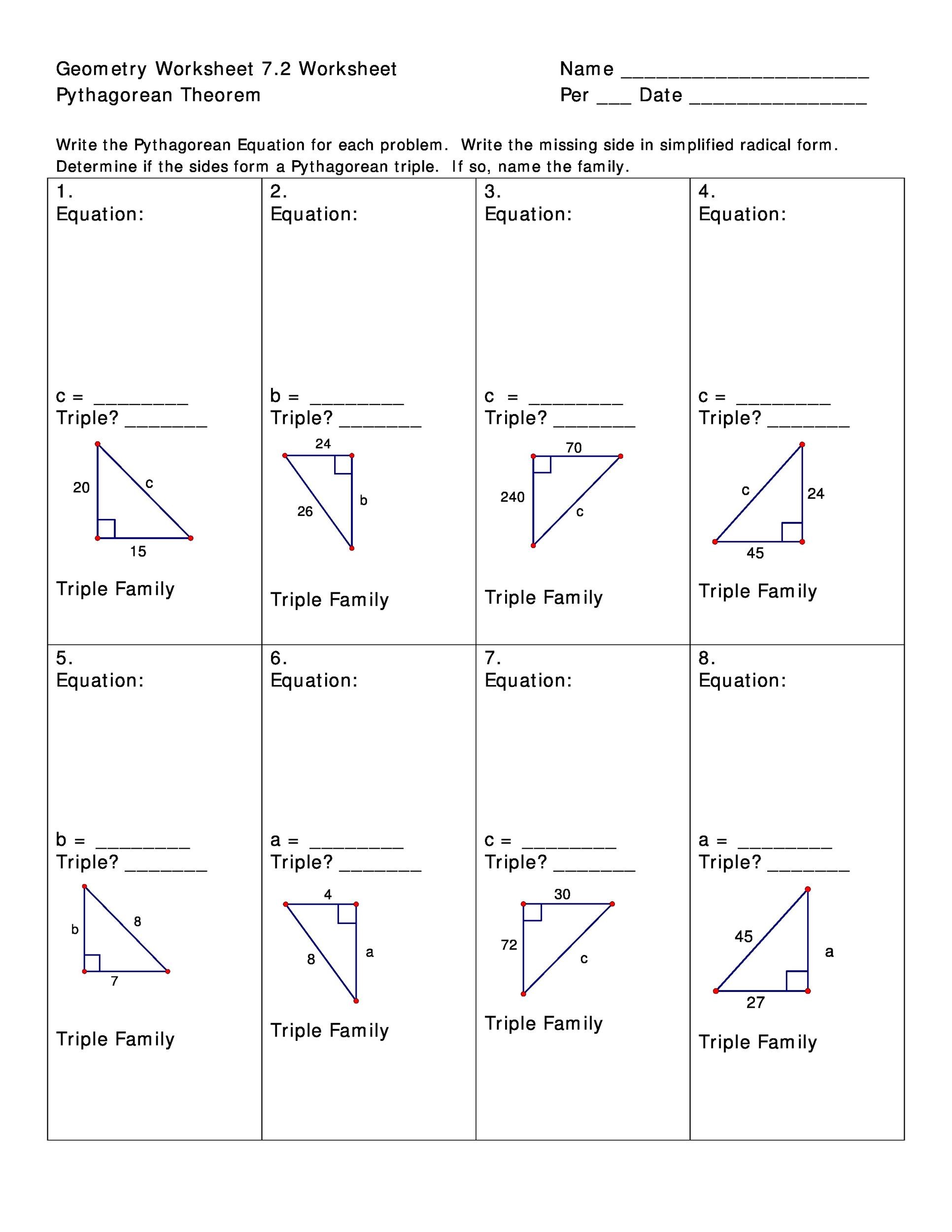
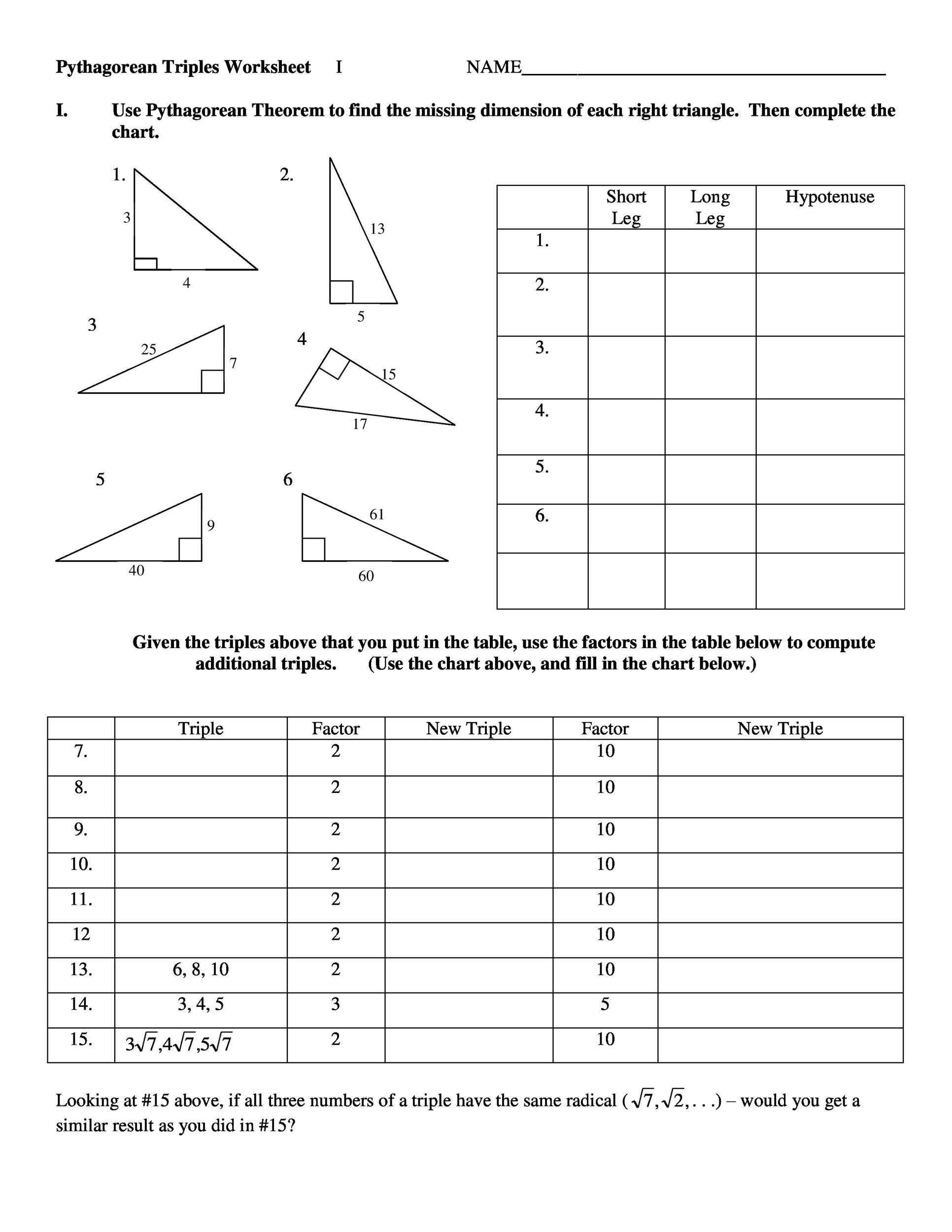
Many Pythagorean triples were known to the Babylonians while the Egyptians knew and used the (3, 4, 5) triple. The Chinese and Indians also played a role in the invention of the Pythagoras Theorem. The first diagrammatic proof of the theorem was produced by the Chinese while the Indians discovered many triples. In 1995, the theorem became part of the Guinness Book of Records as the most proved theorem of all time.
The triples used in the Pythagoras Theorem include (3, 4, 5), (6, 8, 10), (5, 12, 13), (8,15,17), (7,24,25), (20,21,29), (12,35,37), (9,40,41), (28,45,53), (11,60,61), (16,63,65), (33,56,65) and (48,55,73). The aforementioned triples aren’t multiples of a smaller triple and the name given to them is ‘primitive’ triples. To solve a particular problem, the Pythagoras Theorem can be arranged. For example, if you’re asked to find b which is one of the two smaller sides of the right-angled triangle, you can rearrange the theorem to b²=c²-a². By doing this, you’ll be able to easily find the missing value.
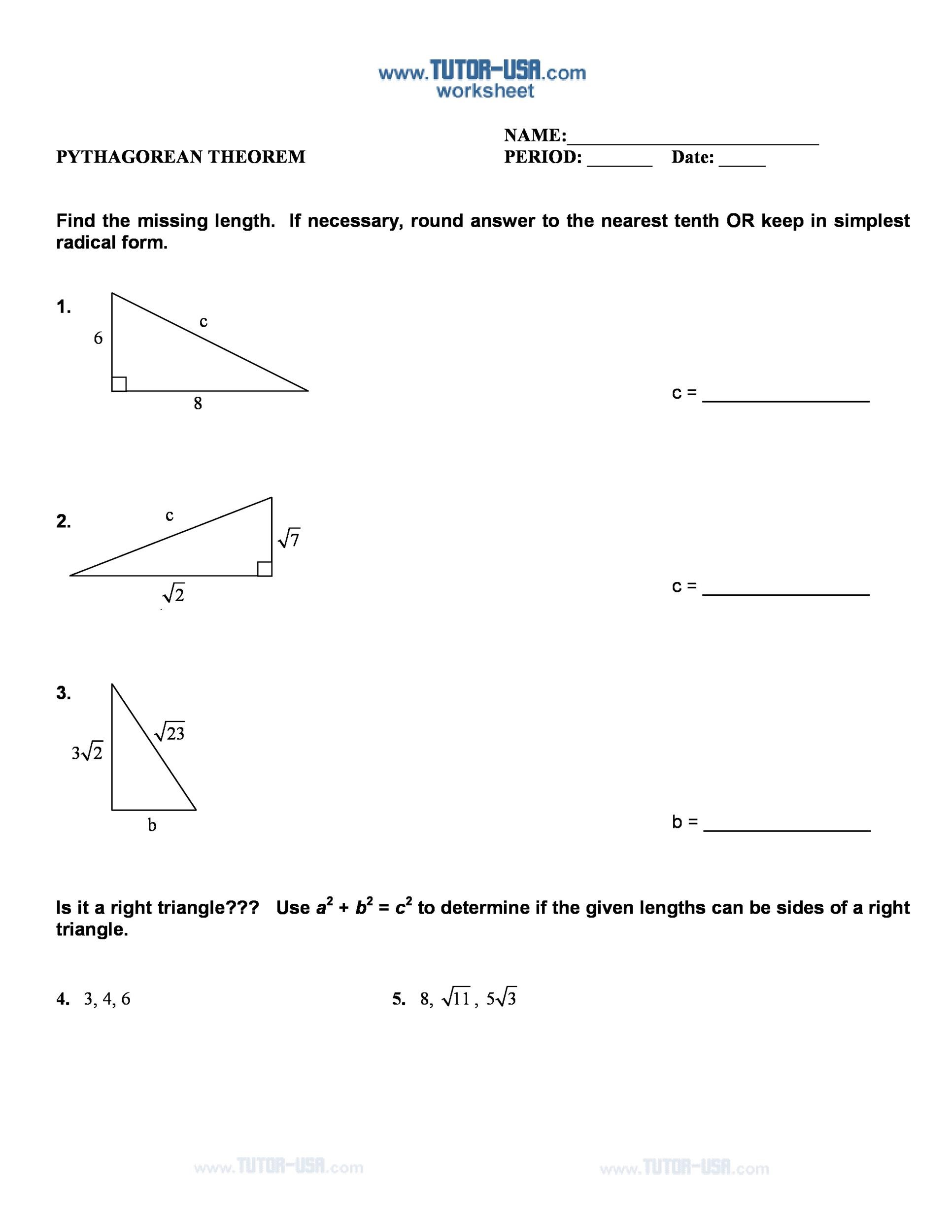
The Pythagoras Theorem has many different proofs. However, when checking your answers, following are the two things that you must always remember:
- The side opposite to the right angle or simply the hypotenuse is always the longest side of the triangle
- Though it is the longest side of the triangle, the size of the hypotenuse can never exceed the sum of the other two squares
To understand this better, take a look at a Pythagoras Theorem worksheet. Today, you can get easy access to Pythagorean Theorem worksheet with answers. Nonetheless, we’re going to try and understand the Pythagoras Theorem as much as we can.
As mentioned earlier, if you know the size of the other two sides, you will be able to find out the length of the third side of the right angle triangle. Also, after being squared, the shorter length is subtracted from the square of the hypotenuse when the hypotenuse is one of the two known lengths. As seen earlier, the lengths of each side of the triangle in the Pythagoras Theorem are whole numbers. Such triangles are known as Pythagorean triangles.
Though there are many different proofs of the Pythagoras Theorem, only three of them can be constructed by students and other people on their own. The first proof starts off as rectangle and is then divided into three triangles that individually contain a right angle. To see first proof, you can use a computer or something as straight forward as an index card cut up into right triangles.
Beginning with a rectangle, the second proof of the Pythagoras Theorem starts off by constructing rectangle CADE with BA=DA. This is followed by the construction of the <BAD’s angle bisector. Once constructed, the bisector is allowed to intersect ED at point F. This makes <BAF and <DAF congruent, BA=DA, and AF=AF. This in turn makes the triangle DAF equal to triangle BAF which means that since ADF is a right angle, ABF will also be a right angle. The third and final proof of the Pythagorean Theorem that we’re going to discuss is the proof that starts off with a right angle. In this proof, triangle ABC is right angle and its right side is angle C.
The three proofs stated above are just few of the many Pythagoras Theorem. You’ll come across these proofs when you take a look at the Pythagorean Theorem worksheet with answers. Learning and understanding the Pythagorean concept is extremely important for students and other people who’ll use this theorem in their practical life.
It is important that you understand the algebraic representation of the Pythagoras Theorem as well as the geometric concepts behind it. You can accomplish this by using proofs, manipulatives, and computer technology. By using these methods to learn Pythagorean Theorem, you’ll be able to see the connections and benefit greatly.
Conclusion
Formulated in the 6th Century BC by Pythagoras of Samos, Pythagoras Theorem is widely used today. If you want to practice Pythagoras Theorem then you can do that easily. Pythagoras Theorem worksheets with answers are easily available and you can use these worksheets to get a good grip of the Theorem.