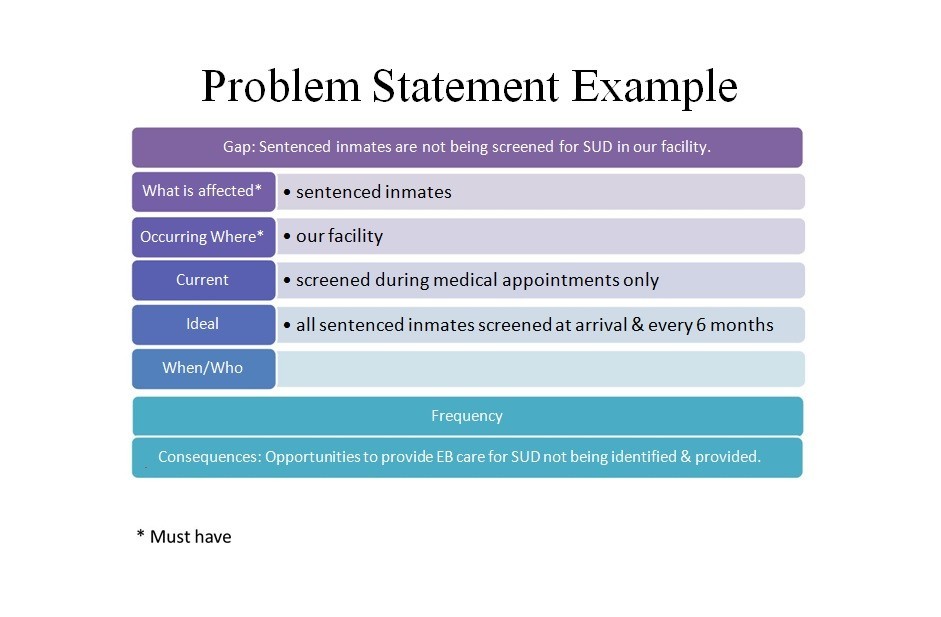
A problem statement is a short description of a problem or an issue which needs addressing or a condition which needs improvement. Making a problem statement template would allow you to identify the gap between the current state or the problem and the desired state or the goal of a product or a process. As this document focuses on the facts, the design of all problem statement examples addresses the 5W’s namely who, what, where, when, and why.
Table of Contents
- 1 Problem Statement Templates
- 2 What is a problem statement?
- 3 Problem Statement Examples
- 4 What are the goals of making a problem statement template?
- 5 Business Problem Statements
- 6 How to write a problem statement template?
- 7 Issue Statement Examples
- 8 Tips for polishing your problem statement template
- 9 Problem Statement Samples
Problem Statement Templates
What is a problem statement?
The first thing to do when you’re trying to solve a problem is to understand it. The best way to do this is through a statement of the problem. A problem statement is all about a specific area of concern, a condition which needs improvement, a difficulty which needs elimination or a troubling query which requires deliberate investigation and meaningful understanding. Organizations and businesses widely make use of business problem statements to execute projects which involve process improvement.
A problem statement template should discuss the gap between the current performance level and the desired performance level. It should contain relative or absolute measures of the issue to quantify the gap. However, it shouldn’t contain possible solutions or causes. Some key elements in such a document include:
- The gap which exists right now.
- The timeframe for solving the problem starting when you first observed it as well as the trend the problem follows.
- The impact of the problem and what you need to quantify the existing gap.
- The importance of finding the solution to the problem to emphasize its urgency.
Problem Statement Examples
What are the goals of making a problem statement template?
The main goal of making a problem statement template is to convert a generalized problem into a well-defined problem which you can focus on. To help you out, you may use this template or look through some issue statement examples so you can have a better idea of what the document contains. After composing the document, you can start resolving the issue through research and some well-thought-out decision-making.
Writing a statement of the problem may help you establish the purpose of a research project clearly. This document can also serve as your basis for the first part of the final proposal that you create. Therefore, it can help direct the reader’s attention to the problem that the project you’re proposing will deal with. This is a fairly simple document which may only need a single page to contain all f the relevant information.
Business Problem Statements
How to write a problem statement template?
As aforementioned, a problem statement gives you a clearer look of the overall method you can use to solve a problem. Therefore, a business problem statement would serve the same purpose but for a business setting. No wonder that field or industry you’re in, you can benefit a lot from making such a document. Here are some steps to guide you as you compose the document:
Think about your vision
If you want to make a decision on what to do to solve the problem, then you should think about your vision. Think about the benefits that may come out of solving the problem at hand. Take some time to write down your vision concisely.
Write down the issue statement
You can use a sentence or two to describe the problem. Specify the issues rather than making a statement without a solution. The issue statement would explain the problem and why it’s important to find a solution to it.
Plan your method for solving the problem
After identifying the problem, the next thing to do is to plan the method for solving it. This is one of the most important parts of the document as you would see in problem statement examples. Through the method, you will explain the steps you plan to take to solve the issue at hand.
The 5W’s
A great problem statement should answer the 5W’s:
- Who: it should explain the specific individuals, groups or organizations that the problem affects.
- What: it should describe the problem’s boundaries, the problem itself, the effect it has, what would happen if the problem gets solved or what would happen if you aren’t able to find a solution.
- When: it should state when the issue started and when you need to solve it.
- Where: it should state where the problem happens whether it’s just in a specific location or in different areas.
- Why: it should talk about the importance of solving the problem and how solving the problem would impact everyone and everything involved in it.
As you answer these questions, this would help you zero in on the issue at hand. Therefore, the problem in your document should be completely solvable. This means that it should take just the right amount of time to come up with a potential solution for it.
After answering all of the questions you’ve thought about, you will have a better grasp of your problem statement. You may have to create a few drafts until you’ve polished your problem statement sufficiently.
Issue Statement Examples
Tips for polishing your problem statement template
If you look at issue statement examples online, you’ll see that they are all brief but informative. This is one of the most important characteristics of problem statement templates. As you compose this document, make sure that you don’t make them longer than it needs to be.
As long as you’ve laid the problem out along with the simple methodology, then you don’t have to add anything else. In fact, adding too much information might end up confusing your readers. When you’re done with the document, it’s important to proofread and polish it as the final steps. Here are some tips to guide you:
- As you go through the content of the document, examine all of the sentences closely. If you find one which doesn’t contribute to the goals of the document directly, omit that sentence. Also, make sure that you only use clear and direct language when composing your sentences.
- When you write this document, you don’t have to add your own “flavor” or personal commentary as this might unnecessarily lengthen the document.
- Keep your audience in mind while you’re writing your problem statement document . Remember that you’re not making this document for yourself, other people will read the document. In most cases, the people who will read your document will have a lot of differences in terms of their knowledge, their reason for reading the document, and their attitude towards the issue at hand. Consider all these people as you compose the document.
- Try to avoid using technical jargon which people might not understand. If you think that you need to use such terms, make sure to define them briefly. In doing this, you can help your audience understand the message you want to convey without confusing them.
- However, if you know that you’re writing for people who have vast technical knowledge of the subject, then you may consider using such jargon. But if you want the document to have better versatility, then it’s best to use simple, direct sentences which anyone will understand.
- As you compose your problem try to make it as defined and as narrow as possible. The best kinds of problem statements are those which don’t ramble on or talk too much about unnecessary things. Rather, they focus on a single problem that’s easy to identify and has a real solution. In reality, narrow and defined topics are much easier to write compared to vague ones. Therefore, you should stick to the scope of your problem whenever possible.
- As a rule of thumb, you should only create a problem statement about an issue which you can solve without a doubt. If you discover that the problem you have doesn’t have a definitive solution, then you can try to narrow down the scope then modify your problem statement making it about your new focus.
- If you want to maintain the scope of your problem statement, you can try completing the content of your proposal first before composing your problem statement. Then you can make use of the actual proposal as your guideline so you don’t have to perform any guesswork.
- Always keep the 5W’s in mind. Problem statement templates should contain as much information as possible but written in a direct and concise way. If you’re not sure about what to make part of the problem statement, try to ask the 5W’s and answer all your own questions. This will provide you with the basic knowledge you need to understand the problem better, as well as the solution without having to add unnecessary details.
- As you write the document, make use of a formal voice just as you would for more serious projects and proposals. Employ a dignified and formal writing style for this document. Maintain the clarity, simplicity, and directness when writing the problem statement. You don’t have to “win over’ your reader by using a casual or friendly tone. Also, never use jokes, humor, anecdotes slang, jargon that’s too technical or pointless details.
- When you’re done, don’t print out the document just yet! Make sure to proofread the document first. This is an important step for any official documents. If you’re making the problem statement with a team, then more than one of you should perform the proofreading to make sure that there aren’t any grammatical or spelling errors.